Introdução à Programação

Uma palavra-chave para entendimento do que seja programação é o conceito de algoritmo, discutido na próxima seção. Um exemplo é algoritmo da multiplicação, sobre o qual existem registros de seu uso há mais de 5.000 anos. Outro exemplo é o algoritmo da divisão utilizado por babilônios (2.500 AC) e por egipcios (1.500 AC).

Neste texto apresentamos a ideia básica do que vem a ser um algoritmo e sua relação com a programação de computadores, apresentando a necessidade de uma linguagem formal e sua contra-parte no computador (via compilador ou interpretador). Também ilustramos exemplos de problemas que deveriam ser resolvidos via algoritmo e, para isso, ainda apresentamos detalhes de programa, como a necessidade de variáveis.

A fim de ilustrar de modo mais concreto a ideia de um programa, lançamos mão de uma linguagem próxima ao Português, por essa razão apelidada de Portugol. Para explicar o código Portugal, usamos o conceito de comentário: um texto após duas barras // (como o trecho da seção 8.1). Exemplos de comandos Portugol:

1. inteiro a,b: comando para declarar uma variável do tipo inteira (no caso a e b);
2. leia(a) : comando para ler um valor e guardá-lo em uma variável (no caso, de nome a);
3. se (EXPRLOG) CMD1 senao CMD2 : comando de seleção (se EXPRLOG resultar verdadeiro, execute comando CMD1, caso contrário execute comando CMD2).

De modo simplificado, um algoritmo é uma sequência finita de passos bem definidos para a realização de uma tarefa. Um exemplo simples, seria a seguinte descrição para se preparar café:

1. preparar o ambiente (separar uma chaleira, um funil com coador e uma garrafa térmica); 2. ferver 1/2 litro de água na chaleira; 3. passar a água da chaleira para a garrafa (para pré-aquecer a garrafa), depois devolver para a chaleira; 4. voltar a ferver a água da chaleira; 5. colocar 2 colheres (de sopa) de pó de café no coador; 6. derramar (sem deixar vazar) a água fervente sobre o pó no coador.

Quando um algoritmo está codificado em um formato que o computador "entende" (i.é., consiga executá-lo), dizemos tratar-se de um programa. Nesse caso, o programa está codificado em linguagem de máquina (linguagem de baixo nível). Por outro lado, se o algoritmo estiver codificado em uma linguagem mais próxima da linguagem humana, dizemos tratar-se de uma linguagem de alto-nível para programação. Alguns exemplos de linguagens de programação são as linguagens C, Python, Java e JavaScript.

A tabela 1 ilustra um trecho de código fonte em uma pseudo-linguagem de programação que usaremos em alguns dos textos e do lado direito, seu código executável correspondente (na verdade dois trechos, as linhas 48, 49 e 108).

55
48 89 e5
48 83 ec 10
48 8d 45 fc
48 89 c6
48 8d 3d a9 0e 00 00
b8 00 00 00 00
e8 db fe ff ff
48 8d 45 f8
48 89 c6
48 8d 3d 91 0e 00 00
b8 00 00 00 00
e8 c3 fe ff ff
8b 55 fc
8b 45 f8
39 c2
7d 18
8b 45 fc
89 c6
48 8d 3d 74 0e 00 00
b8 00 00 00 00
e8 93 fe ff ff
eb 16
8b 45 f8
89 c6
48 8d 3d 5c 0e 00 00
b8 00 00 00 00
e8 7b fe ff ff
b8 00 00 00 00
c9
c3
0f 1f 40 00

Um programa codificado em uma linguagem alto-nível é denominado programa fonte, enquanto o programa em baixo nível é programa executável. O primeiro recebe o nome de fonte por ser a origem do segundo, que é aquele que pode ser executado por um computador, daí a origem do segundo nome.

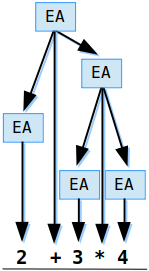
Uma característica importante de qualquer linguagem de programação é a sua sintaxe muito bem definida. Por sintaxe entenda o conjunto de regras a partir das quais podemos reconhecer que um texto nessa linguagem está sintaticamente correto ou não. Para ilustrar, podemos pensar na sintaxe de uma expressão aritmética (EA), por exemplo, se EXPA1 e EXPA2 forem expressões aritméticas sintaticamente corretas, então certamente a nova expressão formada por EXPA1+EXPA2 também será uma EA correta. Assim, uma definição simplificada para expressão, envolvendo apenas somas e produtos (propositadamente estamos ignorando o problema da precedência de operadores), seria

EA := constante EA := EA + EA EA := EA * EA

Entretanto, devemos destacar que enquanto a língua falada permite ambiguidades, uma linguagem de programação não pode admitir isso, pois não seria razoável esperar que um programa (com os mesmos dados de entrada) em determinado momento produza um resultado e noutro produza resultado distinto. Pense no algoritmo da multiplicação, não é admissível que 33 vezes 45, que deveria sempre resultar 1.485, eventualmente obtenha como resposta 4.185.

Um exemplo de frase ambígua na língua Portuguesa seria "essa fruta está verde", que pode significar que a fruta não está madura ou referir-se à cor da fruta (e.g. caiu tinta sobre ela).

Neste texto ilustramos a última etapa do processo de programação usando uma linguagem semelhante ao Português, adotando uma sintaxe derivada da linguagem Algol, por isso denominada Portugol.

Da mesma forma que a sintaxe é importante para existir comunicação entre falantes de uma mesma lingua, toda linguagem de programação deve ter uma sintaxe associada para permitir sua automatização via computador.

Uma vez um programa codificado em linguagem alto nível é compreensível por humanos, para produzir resultados práticos, é essencial que exista um programa executável

Mas como pode-se imaginar, que deve existir um programa (em linguagem de máquina) que consiga traduzir um código em uma linguagem de alto-nível para seu correspondente em baixo nível. Esses programas tradutores podem ser um compilador ou um interpretador.

Fig. 1. Dado um programa fonte, esse precisa ser traduzido para um executável/interpretável.

A grande diferença entre um compilador e um interpretador, é que o primeiro realiza a tradução uma única vez (compilador), enquanto o segundo realiza a tradução toda que executa o código (interpretador).

Como citado acima, o programa codificado na linguagem alto-nível é denominado programa fonte, enquanto o programa em baixo nível é programa executável.

Existem variantes entre ambos os modelos, como na linguagem Java que existe um passo de compilação, que gera um código binário (byte code) que, ao final deve ser interpretado. Nesse modelo pode-se distribuir para quem está interessado em rodar o seu programa, apenas o código binário, ou seja, não é necessário distribuir o código fonte.

Desse modo, outra grande diferença entre linguagens compiladas e linguagens interpretadas é que, se você é um desenvolvedor de software, utilizando uma linguagem compilada, então você pode distribuir apenas a código executável, não precisando divulgar seu código fonte. Já para desenvolver software em linguagem interpretada (como JavaScript), precisará entregar o código fonte.

O modelo de computador atual segue os princípios estabelecidos pelo matemático John von Neumann, no qual tantos dados quanto programa fica na memória, podendo-se alterá-los.

Por ser possível alterar livremente os programas na memória, esse modelo permitiu a construção de linguagens de programação de níveis mais elevados, o que podemos entender como mais uma das aplicações do princípio da alavanca:

1. desenhar uma primeira linguagem de montagem e implementar um programa de baixo nível que consegue traduzir qualquer código correto nessa linguagem para a linguagem de baixo nível;
2. desenhar uma segunda linguagem, em nível mais alto (e.g. a linguagem C) e implementar um compilador para essa linguagem usando a linguagem de montagem anteriormente obtida; e
3. assim por diante até conseguirmos as atuais linguagens de programação.

Fig. 2. Com o princípio da alavanca fica mais fácil "mover o mundo".

Como resultado desse processo de alavancagem, hoje podemos desenvolver software de modo muito mais rápido usando linguagens de alto nível.

A partir da implementação de uma linguagem em computador, pode-se definir uma nova linguagem, codificá-la a partir da primeira e depois gerar uma versão computacional, permitindo programar a partir da segunda linguagem. A primeira linguagem serviu de alavanca para a segunda.

Desse modo, um curso introdutório à programação (IP) visa ensinar os princípios da programação em alguma linguagem de alto nível e isso envolve a capacidade de encontrar soluções algorítmicas para problemas práticos ou teóricos, além de ensinar como codificar e testar o programa-solução que implementa tal algoritmo.

Isso significa que a dificuldade em um curso IP não é meramente "aprender" uma nova "língua", esse aprendizado é necessário, mas não é o que demanda maior esforço para aprendizado. É preciso aprender a encontrar um algoritmo que resolva determinado tipo de problema, considerando qualquer das possibilidades de dados para esse tipo. Os dois primeiros desse processo é ilustrado na figura 3: dado o problema, desenhar um modelo para depois construir sua solução algorítmica.

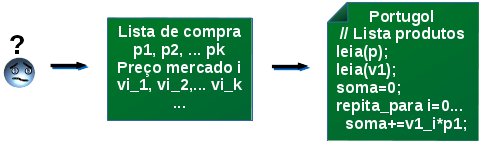
Fig. 3. Os dois primeiro passos a serem aprendidos em um curso introdutório de programação.

Por fim, sua implementação deveria funcionar para todas as possíveis entradas para o problema considerado. Cada entrada pode ser considerada uma instância do problema.
Exemplo 1. Um exemplo seria multiplicar dois números inteiros (armazenados nas variáveis) n1 e n2.
Cada par de inteiros n1 e n2 será uma instância de entradas para o algoritmo. Desse modo, o algoritmo deve funcionar para qualquer par de valores inteiros, não apenas para n1=33 e n2=45.

Assim, programar demandará o aprendizado em três fases: modelar problemas, encontrar algoritmos usando tal modelo e, por fim, implementar esse algoritmo em uma linguagem de programação (e testar se funciona). Cada uma dessas fases tem as suas dificuldades, mas deve-se destacar que uma vez que você aprendeu a programar usando uma linguagem, poderá aprender outra linguagem mais facilmente, poderia focar nas diferenças entre as linguagens (embora essas podem não ser pequenas).

Encontrar o modelo para o problema está associado com a melhor escolha para a estrutura de dados, ou seja, como representar os dados do problema, qual seria a melhor forma para armazenar os dados da instância do problema. Em um curso de introdução são examinadas apenas estruturas de dados básicas, como vetores/listas e matrizes (vide seção 7).

Para ser possível aplicar um algoritmo a uma ampla variedade de distintas entradas é necessário que o algoritmo seja desenhado a partir de valores variáveis, como o já citado algoritmo da multiplicação entre dois números. No exemplo anterior, os termos n1 e n2 são as variáveis, que poderiam armazenar valores que variariam. Os valores para n1 e n2 definem uma instância para o problema da multiplicação e, desse modo, o algoritmo desenhado para multiplicar é aplicável à quaisquer dois valores.

Fig. 4. Ilustração das variáveis n1 e n2, além de re que deverá armazenar o produto dos valores em n1 e n2.

Todas as linguagens de programação de alto nível permite o uso de variáveis e são com elas que podemos armazenar os valores para cada instância do problema. Isso será ilustrado no exemplo 2, com variáveis do tipo vetor ou lista.

Para ilustrar o que você deverá aprender um curso de introdução à programação (IP), na seção seguinte exploraremos um exemplo não trivial envolvendo as 3 fase do problema, encontrar um modelo, desenhar um algoritmo que resolve o problema e depois propor uma implementação (na linguagem que denominamos Portugol. Na próxima seção apresentaremos um modelo com mais um nível de abstração e, portanto, um pouco mais difícil de ser compreendido.

A seção 8 apresenta uma solução para o exemplo 2 abaixo e a seção 9 a solução para o exemplo 3. Em um primeiro estudo, talvez seja recomendável não se preocupar com a seção 8 e, menos ainda, com a 9. Resumidamente, estude a seção 8 apenas se os conceitos desta seção estiverem bastante claros para você, do mesmo, estude a 9 apenas se a 8 estiver muito bem compreendida. Mas se tiver dificuldade com a seção 8, não desita, procure informações com seu professor ou com colegas.

Nos modelos das duas seções seguintes, existe um número arbitrário de variáveis, representando quantidades e preços, por exemplo, n variáveis para quantidades, sendo que esse n pode ser qualquer natural. Desse modo será necessário estender o conceito de variáveis para poder representar uma quantidade arbitrária valores e de preços, a saber, os conceitos de lista (ou vetor) e sua generalização matriz (basicamente uma lista na qual cada um de seus elementos são novas listas):

1. Lista: Uma sequência de variáveis, de nome comum, em posições consecutivas de memória, cujos elementos são recuperados pelos índices (como v[0], v[1], ... v[n-1])
   
   Fig. 5. Ilustração de lista/vetor v[], com 500 elementos (desde v[0] até v[499]) em memória.
   Na memória, como ilustrado na figura 5, as "variáveis de uma lista" ocupam posições contíguas da memória, em particular, note que a variável v[1] guarda o valor 45 e está imediatamente à esquerda (na memória) da variável v[2], que guarda o valor 1.
2. matriz: Uma sequência de listas, de nome comum, em posições consecutivas, recuperados por dupla indexação, assim se a matriz tiver m linhas e n colunas, as variáveis da linha 0 vão de m[0][0] até m[0][n-1] e da última linha (linha m-1) vão desde m[m-1][0] até m[m-1][n-1].
   
   Fig. 6. Ilustração de matriz m[][], com 600 elementos em 30 linhas, cada uma com 20 colunas - desde m[0][0] até m[29][19].
   Cada linha de uma matriz é uma lista e as linhas i e i+1 também são contíguas na memória. Na figura 6 apresentamos uma matriz de nome m, com 30 linhas e 20 colunas. Assim, as linhas 0 e 1 são listas consecutivas na memória, portanto o último elemento da linha 0 (variável m[0][19]) está imediatamente à esquerda do primeiro elemento da linha 1 (variável m[1][0]), ou seja, a variável m[0][19] guarda o valor 91 e está imediatamente à esquerda da variável m[1][0], que no exemplo está guardando o valor -1.

Exemplo 2. Uma pessoa deseja um programa que compute seus gastos em determinado mercado. Os dados de entrada são as quantidades de cada produto desejado (a cesta)e seus respectivos preços no mercado, a saída deverá ser quanto gastará a cesta de produtos.

Assim, no exemplo 2 o objetivo é saber quanto custa em um determinado marcado a cesta de produto. Então, podemos imaginar um generalização desse problema, tendo a disposição uma lista de mercados, cada um com seus particulares preços de produtos.

Exemplo 3. Uma pessoa deseja um programa que indique em qual mercado deveria comprar. Os dados de entrada são as quantidades de cada produto desejado (a cesta) e seus respectivos preços em uma lista de mercados, a saída deverá ser quanto gastará em cada mercado (visando, depois selecionar aquele de menor preço).

Assim, resolver esse problema na forma de algoritmo não seria meramente computar qual dos mercados teria "o menor valor para a lista de compra desejada naquele momento", mas encontrar uma solução que possa ser aplicada a outros produtos e mercados. Ou seja, deveria funcionar para qualquer instância do problema (para qualquer lista de compra e para qualquer lista de mercados).

Analisando o exemplo 2, o programa a ser desenvolvido precisa receber uma lista com as quantidades de cada produto desejado e quanto custa cada unidade em determinado mercado.

Podemos imaginar que o interssado tenha conseguido os dados sobre os preços de cada produto via Internet e, como a quantidade de produtos é arbitrária, devemos desenvolver um programa que permita essa generalização. Desse modo, é rezoável usar uma lista para representar as quantidades desejadas (q[0..n-1]) e uma lista para os valores de cada unidade de produto no mercado (v[0..n-1]).

Assim, o programa deve computar a soma do custo de todos os projetos, portanto a variável que conterá a resposta pode ser chamada de soma. Ao final deveremos ter soma = q[0]*v[0] + q[1]*v[1] +...+ q[n-1]*v[n-1].

Porém o computador realizar apenas uma operação por vez, precisamos desenhar uma solução que no primeiro passo compute q[0]*v[0], no passo 2 acumule q[1]*v[1] e assim por diante até q[n-1]*v[n-1]. Para acumular, considerando um passo genérico i, devemos usar a instrução:

Dada a importância desse conceito, vamos destacá-lo como uma definição.
Uma variável de acumulação é aquela que recebe o que ela guardava (até então) somado ao resultado de alguma expressão aritmética, ou seje,

Deste modo, basta iniciar a variável acumuladora soma com o valor 0 e a primeira vez que a instrução soma <- soma + q[i]*v[i] for executada ela funcionará bem: soma <- soma + q[0]*v[0].

A atribuição acima deve ser feita n vezes, então podemos usar a ideia de laço de repetição ou apenas laço. As linguagens de programação dispõem de mais de um comando para controlar laços, usaremos um que tem uma quantidade de passos previamente conhecido, um laço do tipo repita_para, mas em várias linguagens é apenas o comando for: repita_para i de 0 ate n // repete os comandos subordinaos n vezes

Assim, usando um laço controlando a variável i, iniciando-a com o valor 0 e seguindo incrementando-a com mais uma unidade, n vezes, teremos um programa completo que resolve o problema. Vamos prever a entrada de dados, o numero de produtos n, as quantidades de produtos desejados (q[0] até q[n-1]) e os custos unitários de cada produto (v[0] até v[n-1]).

// Leitura dos dados com quantidades de produtos desejados e total de mercados:
leia(n); // usuario devera' digitar quantos produtos deseja
repita_para i de 0 ate n // digitar quantidades desejada de cada produto
  leia(q[i]); // entrada da qde do produto i
repita_para i de 0 ate n // digitar o valor de cada produto no mercado considerado
  leia(v[i]); // entrada do valor unitario do produto i

// variavel para acumular o custo total desde o primeiro produto (q[0]*v[0]) ate' o atual (q[i]*v[i])
soma <- 0; // variavel para acumular o custo de cada produto

// Bloco para computar o custo total
repita_para i de 0 ate n { // para cada produto i
    soma <- soma + q[i]*v[i]; // acumule custo produto i
    } // final do laco "repita_para i"
// avise ao usuario o quanto ele gastara'
escreva("Total a ser gasto", soma);

O problema associado ao exemplo 3 generaliza o exemplo do 2, pois no 3 devemos considerar a existẽncia de preços em vários mercados.

Desse modo, o modelo consideraria a existência de duas listas, uma lista de produtos (q[0] unidades do produto 0, q[1] unidades do produto 1 e assim por diante) e uma lista de preços desses produtos em cada mercado, o que pode ser representado por uma matriz cuja linha i conterá os preços no mercado i. No exemplo 2 usamos apenas uma lista de preços, pois havia apenas um mercado.

Vamos supor termos N produtos e M marcados, assim precisamos de uma matriz de preços p[N][M]:

Até o final de um curso de IP você deve ser capaz de desenhar o modelo acima e de conseguir visualizar a sua solução na forma de um algoritmo. Mas para você ter uma ideia do que se deve aprender em IP, apresentamos o processo de construção desse algoritmo.

O objetivo dessa seção é apresentar uma solução para o problema de encontrar o "melhor" mercado a comprar e talvez seja dificil entender completamente o processo. O mais importante é tentar perceber a ligação do algoritmo com o modelo (o tratamento das variáveis).

Passo 1. Deve-se tentar desenhar o algoritmo de modo construtivo.

Podemos pensar em computar para o mercado 0, para o mercado 1 e assim por diante. Entretanto já resolvemos problema semelhante para um mercado, vamos tentar generalizar.

Passo 2. Depois poderiamos fazer a mesma coisa para o mercado 2, 3 e assim por diante.

O problema envolve a necessidade de tratar a "cesta de compra", a lista do que deve ser comprado (que nomeamos q[.]), conseguir saber o preço da "cesta" em cada mercado e, ao final, ter determinado o menor preço (em que mercado comprar?).

Como no problema anterior, para cada mercado i, devemos usar um laço de repetição para determinar quanto custa a "cesta" de compras ali. Se usarmos novamente a variável soma para computar isso deveremos, para cada mercado, executar a instrução abaixo:

repita_para j de 0 ate n { // Laco_mercado_j: para cada mercado j
    soma <- soma + q[j]*p[i][j]; // acumule custo produto i
    } // final do laco "repita_para j"

Entretanto, existem M mercados e objetivo é ficar com o preço do menor. Mas podemos "abstrair", suponha termos em uma variável soma_min a menor soma e em melhor_mercado o número do merco que gerou essa menor soma. Assim, bastaria ao final do laço Laco_mercado_j, verificar se aquela soma é menor que o mínimo até então, se for teremos um novo mínimo, caso contrário, ignore esse mercado (tem preço maior ou igual ao mínimo até aqui):

Passo k. Generalizar (geralmente associado à uma indução finita)

Usando um princípio de álgebra elementar, a transitividade (a<b e b<c então a<c), podemos estender a ideia acima para um passo genérico k, conseguindo o "menor preço dentre os k primeiros mercados".

Para completar o algoritmo, basta fazer uma inicialização correta para soma_min e melhor_mercado e definir o laço externo, variando para cada mercado. Nesse problema não apresentaremos a parte do algoritmo para a entrada de dados, mas seria semelhante à do problema 1.
Vale destacar que, deste modoe, este problema envolver laço duplo (laço de repetição dentro de outro laço).

// variavel que devera a cada passo ter menor soma e indice de melhor merc
soma_min <- 999999999; // truque: coloque maior valor possivel
melhor_mercado <- -1; // nao sabemos qual o melhor, deixar indice inexistente

// Bloco para determinar melhor mercado
repita_para i de 0 ate M { // para cada mercado i digitar os valores de todos os N prod 
  soma <- 0; // variavel para permitir calculo dos N produtos no marc i 
  repita_para j de 0 ate N { // laco para calcular soma de compra no merc i
    soma <- soma + q[j]*p[i][j]; // acumule custo prod 0 ate' j no merc i
    } // final do laco "repita_para j"
  // nesse ponto soma tem o custo total no merc i - veja se e' menor ate' agora
  se (soma<soma_min) { // redefina menor: mercado i ganha ate' aqui
     soma_min <- soma; // armazene menor soma ate' o passo i
     melhor_mercado <- i;  // armazene indice do melhor mercado
     } // redefiniu "melhor" merc
  } // final do laco "repita_para i"
// avise ao usuario qual o indice do "melhor" merc e qual o menor soma de compra
escreva("Menor preco foi alcancado no mercado", melhor_mercado);
escreva("Menor preco total de compra foi", soma_min);

Neste texto apresentamos: a ideia de algoritmo, de linguagens e de programa de computador; o que vem a ser uma linguagem e sua sintaxe; o que é um compilador e um interpretador (para alguma linguagem); o princípio da alavanca para gerar linguagens de nível mais alto; neste contexto o que significa programar (codificar um algoritmo); a necessidade de variáveis para programar; as 3 fase para resolver um problema na forma de algoritmo; um primeiro exemplo de problema e sua solução; um segundo exemplo de problema e sua solução.

Leônidas de Oliveira Brandão
http://line.ime.usp.br

Alterações :
2024/11/30: melhor explicação para exemplos 2 e 3; acerto de nome de variável (de 'valor' para 'soma');
2024/04/05: melhor estrutura a partir de sugestões do Ian Gabriel (MAC110-2024);
2024/03/08: numeração de seções/h3; acertos léxicos; seçao 8 desmembrada em 8 e 9
2023/03/22: acertos no codigo final
2022/08/17: pequenos acertos
2021/04/10: primeira versão